대칭키 암호는 암/복호화에 같은 키를 사용하기 때문에 송신자와 수신자는 각각 동일한 비밀키를 공유하여야 하며, 키 공유 과정에서의 문제를 해결하기 위해 다음 4가지의 방법을 사용하고 있다.
* 키 배송 문제를 해결하기 위한 방법 4가지
① 키의 사전 공유에 의한 해결
② 키 배포센터에 의한 해결
③ Diffie-Hellman 키 교환에 의한 해결
④ 공개키 암호에 의한 해결
① 키의 사전 공유에 의한 해결
- 송신자와 수신자 간의 비밀키를 미리 협상하는 것을 PSK(Pre-Shared Key)라 한다. 미리 키를 교환하기 때문에 키 배송문제를 쉽게 해결할 수 있지만 통신 대상이 많으면 많을수록 더 많은 키의 관리가 필요하다.
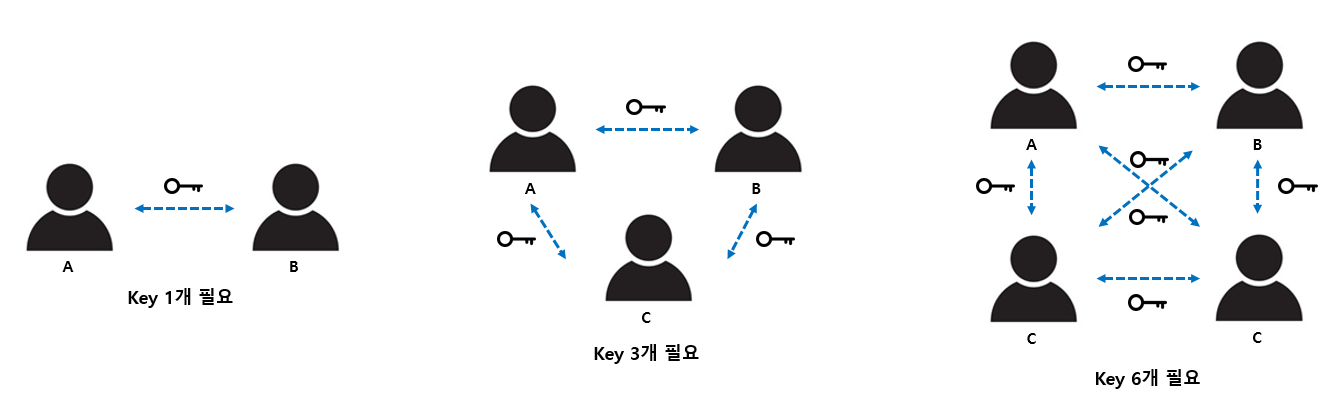
사용자 n명일 경우 키의 개수는 n(n-1)/2
② 키 배포센터에 의한 해결
- 키 분배 센터(KDC)를 이용하여 송신자와 수신자간의 비밀키를 각각 전달한다.
KDC 키 분배 과정에서 사용하는 키는 마스터키(K)와 세션키(S)가 있다.
마스터키(K) : 키 분배 센터와 사용자가 공유하는 유일한 키이다. 사용자가 n명일 경우 키의 개수는 2n개이다.
세션키(S) : 두 사용자간의 암호화 통신을 위한 임시키로 논리적인 연결이 종료되면 폐기된다. 키 분배 센터로부터 마스터키로 암호화되어 전송받는다. 사용자가 n명일 경우 키의 개수는 n개이다.

A -> KDC
① A가 KDC에게 A와 B의 통신을 위한 세션키를 요구한다. 요구 메시지에는 A,B의 신원 요청, A 자신의 ID값이 포함되어있다.
KDC –> A, B
② KDC는 세션키를 생성하고 A와 B의 마스터키를 이용하여 각각 세션키, A, B의 신원정보(ID), Timestamp(T)를 담아 암호화하여 전송한다.
* 이 과정에서 B는 A가 자신과 통신하고자 함을 확인함.
A와 B는 각각 KDC와 서로 공유하고 있던 A, B의 마스터키로 암호화된 키값을 자신의 마스터키로 복호화하여 세션키를 얻는다.
A -> B
③ A는 세션키로 암호화하여 B에게 자신의 ID, Timestamp(T)를 전송한다.
B -> A
④ B는 세션키로 암호화하여 A에게 자신의 ID, Timestamp+1을 전송한다.
③ Diffie-Hellman 키 교환에 의한 해결
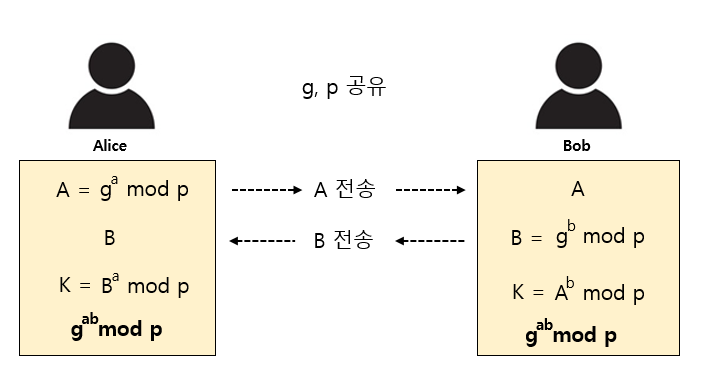
교환 절차
1) Alice는 소수p, 그리고 1부터 p-1까지의 정수 g를 선택하여 사전에 Bob과 공유한다.
2) Alice는 0보다 크거나 같고 p-1보다 작은 정수 a를 선택한다. a는 공유하지 않는다.
3) Alice는 A=g^a mod p를 계산한다.(g^a를 p로 나눈 나머지)
4) Alice는 A를 Bob에게 전송한다.
5) Bob은 0보다 크거나 같고 p-1보다 작은 정수 b를 선택한다.
6) Bob은 B=g^b mod p를 계산한다.(g^b를 p로 나눈 나머지)
7) Bob은 B를 Alice에게 전송한다.
8) Alice는 B^a mod p를, Bob은 A^b mod p를 계산한다.
B^a mod p = (g^b)^a mod p = g^ab mod p
A^b mod p = (g^a)^b mod p = g^ab mod p
따라서 g^ab mod p라는 공통의 비밀키(K)를 공유한다.
④ 공개키 암호에 의한 해결
- 암/복호화에 서로 다른 키를 사용
- 송신자는 수신자의 공개키를 이용하여 암호화, 수신자는 자신의 개인키로 복호화 가능
- 수학적 난제를 기반으로 설계

① 수신자는 공개키, 개인키 중 공개키를 공개함
② 송신자는 수신자의 공개키를 획득
③ 송신자는 문서를 수신자의 공개키로 암호화하여 수신자에게 전송
④ 수신자는 자신의 개인키로 암호화된 문서를 복호화함
'자격증 > 정보보안기사' 카테고리의 다른 글
| 대칭키 DES (0) | 2024.02.22 |
|---|---|
| 공개키 암호 알고리즘 (0) | 2024.02.20 |
| SSL/TLS (0) | 2024.02.16 |
| FTP (1) | 2024.02.15 |
| 대칭키 암호 vs 공개키 암호 (0) | 2024.02.14 |